Las líneas paralelas son dos o más líneas que nunca se intersectan. Hay ejemplos de líneas paralelas a nuestro alrededor, en los dos lados de ésta página y en los estantes de un librero. Cuando ves líneas paralelas o estructuras que aparentan seguir la misma dirección, nunca se cruzan unas a otras, y la distancia entre ellas es constante, es muy probable que sean líneas paralelas.
En álgebra, usamos algo más preciso que la apariencia para reconocer y crear líneas paralelas. Usamos ecuaciones.
Reconociendo Rectas Paralelas
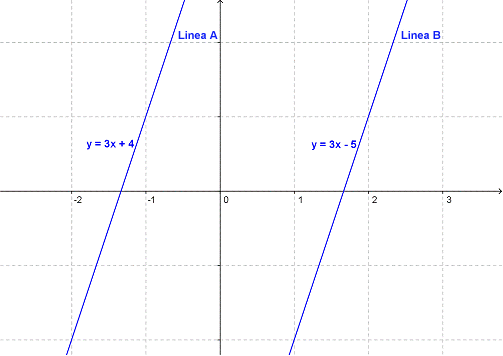
Veamos la siguiente gráfica donde hay dos líneas paralelas.
La línea A tiene la ecuación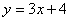 
. La línea B tiene la ecuación 
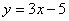. ¿Puedes identificar qué es lo que éstas dos líneas tienen en común?
Intenta comparando los coeficientes de x en cada ecuación. Ambos son 3. Ya que las dos ecuaciones están escritas en la forma pendiente-intersección de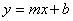 
, el coeficiente x es la pendiente de las líneas. Como la línea A y la línea B tienen pendiente 3, ambas tienen la misma pendiente.
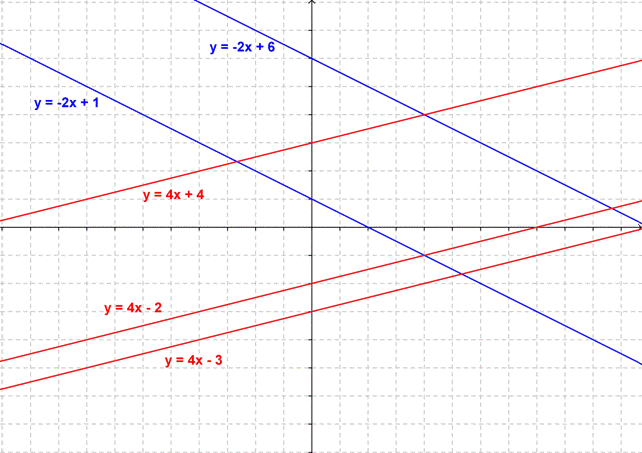
Hemos descubierto una relación que es válida para todas las líneas paralelas — las líneas son paralelas si tienen la misma pendiente. ¿No te convence? Veamos las líneas de la siguiente gráfica:
Las líneas azules son paralelas — van en la misma dirección, mantienen la misma distancia entre ellas, y nunca se tocan — y tienen la misma pendiente. Las tres líneas rojas comparten su pendiente, y también so paralelas la una con las otras. Las líneas azules y las rojas no son paralelas, y tienen pendientes distintas.
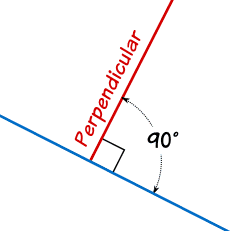
Perpendiculares
Simplemente significa en ángulos rectos (90°) con.
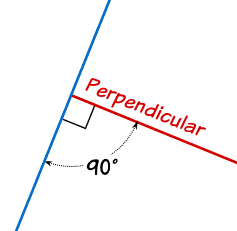
La línea roja es perpendicular a la azul en estos dos casos:
(La cajita en la esquina significa "en ángulos rectos", así que no hacía falta poner también que son 90°, ¡pero queríamos hacerlo!)
